Page 4 - Giáo trình Giải tích

2
2
2
Tập xác định = {( , ) ∈ ℝ |1 − − ≥ 0}, chính là hình tròn có tâm
là gốc tọa độ, bán kính bằng 1.

Hình 1.1
Tập giá trị = √1 − − , vậy T={z∈ ℝ| z≥0}.
2
2
Đồ thị của hàm hai biến
Hàm điểm
Xét hàm số f: (x,y)  f(x,y).
Với mỗi cặp số thực (x,y) xác định một điểm M(x,y) trong không gian hai
chiều Oxy nên ta có thể xem hàm 2 biến f(x,y) là hàm của điểm M(x,y):
f: M  f(M)
Với mỗi điểm M(x,y) trong mặt phẳng Oxy qua hàm f ứng với 1 điểm P(x,y,z)
trong không gian 3 chiều với z =f(x,y).
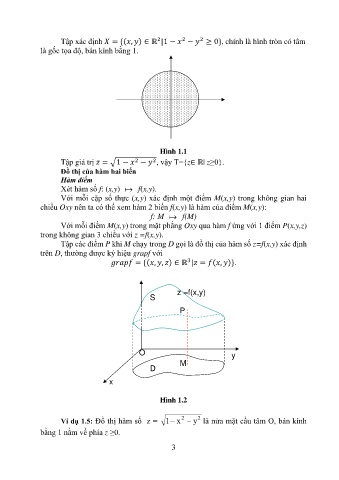
Tập các điểm P khi M chạy trong D gọi là đồ thị của hàm số z=f(x,y) xác định
trên D, thường được ký hiệu grapf với
3
= {( , , ) ∈ ℝ | = ( , )}.

z =f(x,y)
S
P

O y
D M

x

Hình 1.2

2
2
Ví dụ 1.5: Đồ thị hàm số z = 1− x − y là nửa mặt cầu tâm O, bán kính
bằng 1 nằm về phía z ≥0.

3