Page 32 - Giáo trình Giải tích

6) Nếu m là GTNN, M là GTLN của f(x,y) trên D, khi đó

≤ ∬ ( , ) ≤

7) (Định lý giá trị trung bình)
Giả sử hàm f(x,y) liên tục trên miền liên thông D (đóng, giới nội) thì trên D
tồn tại ít nhất một điểm M(x o,y o) sao cho

∬ ( , )
( , ) = .
0
0

2.1.2. Cách Tính

Việc tính tích phân bội hai trực tiếp từ định nghĩa rất phức tạp. Ở đây ta đưa
ra cách tính tích phân bội hai bằng cách dựa vào ý nghĩa hình học của nó.
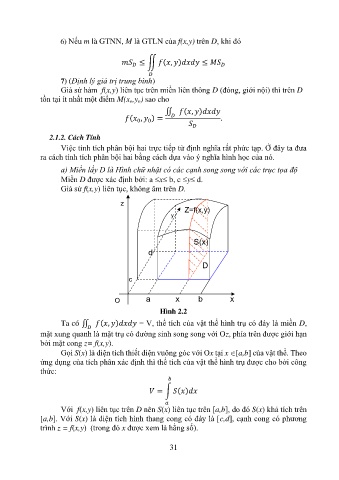
a) Miền lấy D là Hình chữ nhật có các cạnh song song với các trục tọa độ
Miền D được xác định bởi: a x b, c y d.
Giả sử f(x,y) liên tục, không âm trên D.

z
Z=f(x,y)
y

S(x)
d

D

c

O a x b x

Hình 2.2

Ta có ∬ ( , ) = V, thể tích của vật thể hình trụ có đáy là miền D,

mặt xung quanh là mặt trụ có đường sinh song song với Oz, phía trên được giới hạn
bởi mặt cong z= f(x,y).
Gọi S(x) là diện tích thiết diện vuông góc với Ox tại x [a,b] của vật thể. Theo
ứng dụng của tích phân xác định thì thể tích của vật thể hình trụ được cho bởi công
thức:

= ∫ ( )

Với f(x,y) liên tục trên D nên S(x) liên tục trên [a,b], do đó S(x) khả tích trên
[a,b]. Với S(x) là diện tích hình thang cong có đáy là [c,d], cạnh cong có phương
trình z = f(x,y) (trong đó x được xem là hằng số).

31