Page 34 - XSTK6

c) Hàm mªt đë xác su§t

Hàm phân phèi xác su§t F(x) không cho bi¸t rõ phân phèi xác su§t ð lân
cªn mët điºm nào đó trên tröc sè. Vì vªy đèi vîi các BNN liên töc, có F(x) kh£
vi, ngưíi ta đưa ra khái ni»m sau đây.

Đành nghĩa 2.2. Hàm mªt đë xác su§t cõa BNN liên töc X, kí hi»u là
f(x), có hàm phân phèi F(x) kh£ vi (trø ð mët sè húu h¤n điºm gián đo¤n bà
ch°n), đưñc xác đành b¬ng
0
f(x) = F (x). (2.3)
Tø đành nghĩa trên ta th§y n¸u X là BNN ríi r¤c thì hàm phân phèi xác
su§t cõa X là hàm gián đo¤n nên F(x) không kh£ vi t¤i nhúng điºm gián đo¤n. Vì
vªy BNN ríi r¤c không có hàm mªt đë xác su§t.
Ngoài ra, tø (2.3) ta có

x b
Z Z
F(x) = f(x)dx và P(a ≤ X < b) = f(x)dx.
−∞ a

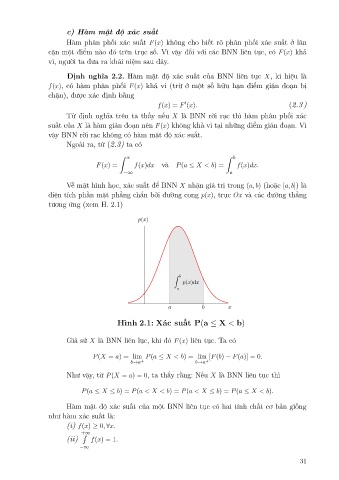
V· m°t hình håc, xác su§t đº BNN X nhªn giá trà trong (a, b) (ho°c [a, b]) là
di»n tích ph¦n m°t ph¯ng ch­n bði đưíng cong p(x), tröc Ox và các đưíng th¯ng
tương ùng (xem H. 2.1)

Hình 2.1: Xác su§t P(a ≤ X < b)

Gi£ sû X là BNN liên löc, khi đó F(x) liên töc. Ta có

P(X = a) = lim P(a ≤ X < b) = lim [F(b) − F(a)] = 0.
b→a + b→a +

Như vªy, tø P(X = a) = 0, ta th§y r¬ng: N¸u X là BNN liên töc thì

P(a ≤ X ≤ b) = P(a < X < b) = P(a < X ≤ b) = P(a ≤ X < b).

Hàm mªt đë xác su§t cõa mët BNN liên töc có hai tính ch§t cơ b£n gièng
như hàm xác su§t là:

(i) f(x) ≥ 0, ∀x.
+∞
R
(ii) f(x) = 1.
−∞
31