Định nghĩa

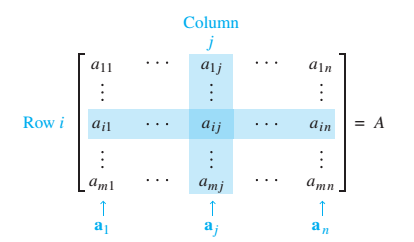
Một ma trận cấp $m\times n$ trên $\mathbb R$ là một bảng số gồm $m\times n$ phần tử trong $\mathbb R$ được viết thành $m$ dòng và $n$ cột (xem hình bên).

Kí hiệu $A=[a_{ij}]_{m\times n}$ hoặc $A=(a_{ij})_{m\times n}$ hoặc $A\in\mathcal M_{m\times n}$
$a_{ij}$: phần tử hàng $i$, cột $j$.
$(a_{ij})_{n\times n}$ là ma trận vuông cấp $n$; các phần tử $a_{11}, a_{22},\cdots, a_{nn}$ là các phần tử trên đường chéo chính.

Các dạng đặc biệt

1. Ma trận hàng: $\begin{bmatrix} a_{11}&a_{12}&\cdots&a_{1n}\end{bmatrix}$.

2. Ma trận cột: $\begin{bmatrix} a_{11}\\a_{21}\\\vdots\\a_{n1}\end{bmatrix}$.

3. Ma trận Không: $(a_{ij}=0)_{m\times n}$, $\forall i,j$.

4. Ma trận chéo: $a_{ij}=0$, $\forall i\neq j$.

5. Ma trận đơn vị: $I_n=\begin{bmatrix}
1&0&\cdots&0\\
0&1&\cdots&0\\
\vdots&\vdots&\ddots&\vdots\\
0&0&\cdots&1\\
\end{bmatrix}_{n\times n}$.

6. Ma trận tam giác dưới: $\begin{bmatrix}
a_{11}&0&\cdots&0\\
a_{21}&a_{22}&\cdots&0\\
\vdots&\vdots&\ddots&\vdots\\
a_{n1}&a_{n2}&\cdots&a_{nn}\\
\end{bmatrix}_{n\times n}$.

7. Ma trận tam giác trên: $\begin{bmatrix}
a_{11}&a_{12}&\cdots&a_{1n}\\
0&a_{22}&\cdots&a_{2n}\\
\vdots&\vdots&\ddots&\vdots\\
0&0&\cdots&a_{nn}\\
\end{bmatrix}_{n\times n}$.

8. Ma trận đối xứng: $a_{ij}=a_{ji}$ với mọi $i,j$. Chẳng hạn: $A=\begin{pmatrix}1&3&2\\3&0&-1\\2&-1&-2\\\end{pmatrix}$