a) Ma trận bằng nhau
Cho $A, B\in \mathcal M_{m\times n}$. Khi đó $A=B\Leftrightarrow a_{ij}=b_{ij},\forall i, j$.
Cho $A, B\in \mathcal M_{m\times n}$. Khi đó $A=B\Leftrightarrow a_{ij}=b_{ij},\forall i, j$.
Cho 2 ma trận $A=\begin{bmatrix}1&0\\1&-1\end{bmatrix}$ và $B=\begin{bmatrix}a&b\\c&d\end{bmatrix}$. Xác định $a,b,c,d$ để $A=B$?
Để $A=B$ thì $a=c=1, b=0$ và $d=-1$.
Cho $A, B\in\mathcal M_{m\times n}$. Khi đó $A+B=(a_{ij}+b_{ij})_{m\times n}$.
Tính chất
$A+B=B+A$
$(A+B)+C=A+(B+C)$
$A+O=A$.
Cho $A=\begin{bmatrix}2&3&5\\-1&4&0\\\end{bmatrix}$ và $B=\begin{bmatrix}5&7&-5\\2&-3&1\\\end{bmatrix}$. Tính $A+B$.
$A+B=\begin{bmatrix}2+5&3+7&5+(-5)\\-1+2&4-3&0+1\\\end{bmatrix}=\begin{bmatrix}7&10&0\\1&1&1\\\end{bmatrix}$.
Cho $A\in\mathcal M_{m\times n}$ và $k\in\mathbb R$. Khi đó $kA=(ka_{ij})_{m\times n}$.
Tính chất. Cho $\alpha, \beta\in\mathbb R$ và $A,B\in\mathbb R$. Khi đó:
$(\alpha\beta)A=\alpha(\beta A)$,
$(\alpha+\beta)A=\alpha A+\beta A$,
$\alpha(A+B)=\alpha A+\alpha B$.
Chú ý. $-A=(-1)\cdot A$.
Cho $A=\begin{bmatrix}3&4\\7&-2\\\end{bmatrix}$. Tính $2\cdot A$.
$2\cdot A=\begin{bmatrix}2.3&2.4\\2.7&2.(-2)\\\end{bmatrix} =\begin{bmatrix}6&8\\14&-4\\\end{bmatrix}$.
Cho $A\in\mathcal M_{m\times n}$. Khi đó ma trận chuyển vị của $A$, kí hiệu là $A^T=(a_{ji})_{n\times m}$.
Tính chất. Cho $A,B\in\mathbb M_{m\times n}$. Khi đó:
Cho $A=\begin{bmatrix}1&0&2\\3&-1&-2\\\end{bmatrix}$. Tính $A^T$.
Ta có $A^T=\begin{bmatrix}1&3\\0&-1\\2&-2\\\end{bmatrix}$.
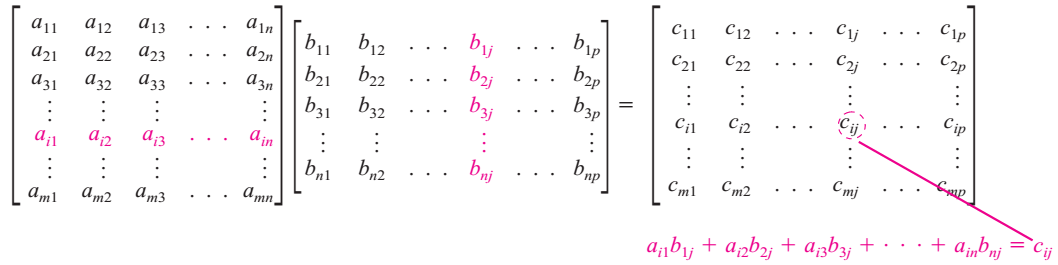
| Cho $A\in\mathcal M_{m\times n}$ và $B\in\mathcal M_{n\times p}$. Khi đó $A\cdot B=C\in\mathcal M_{m\times p}$. Trong đó $$c_{ij}=a_{i1}b_{1j}+a_{i2}b_{2j}+\cdots+a_{in}b_{nj}.$$ |
|
Tính chất: Cho $A,B, C$ là các ma trận với kích cỡ sao cho phép toán có nghĩa và $\alpha\in\mathbb R$ ta có
Cho $A=\begin{bmatrix}1&-1\\-1&1\\\end{bmatrix}$ và $B=\begin{bmatrix}1&1\\2&2\\\end{bmatrix}$. Tính $A\cdot B$ và $B\cdot A$ và rút ra nhận xét.
Ta có: $$A\cdot B=\begin{bmatrix}1.1+(-1).2&1.1+(-1).2\\(-1).1+1.2&(-1).1+1.2\\\end{bmatrix}=\begin{bmatrix}-1&-1\\1&1\\\end{bmatrix},$$ $$B\cdot A=\begin{bmatrix}1.1+1.(-1)&1.(-1)+1.1\\2.1+2.(-1)&2.(-1)+2.1\\\end{bmatrix}=\begin{bmatrix}0&0\\0&0\\\end{bmatrix}.$$
Nhận xét: