Áp dụng định nghĩa phép nhân 2 ma trận.
Cho 2 ma trận $A=\left[a_{ij} \right]_{m\times p} $, $B=\left[b_{ij} \right]_{p\times n} $. Tích của A với B là ma trận cỡ $m\times n$\[AB=\left[\sum _{k=1}^{p}a_{ik} b_{kj} \right]_{m\times n} \; \] Chú ý
Để thực hiện được phép nhân 2 ma trận A với B thì số cột của ma trận A phải bằng số hàng của ma trận B.
Muốn có phần tử $c_{ij} $ trong ma trận tích AB ta tìm tổng tất cả các tích của các phần tử ở hàng i của A (ma trận phía bên trái) và các phần tử tương ứng ở cột j của B (ma trận phía bên phải), theo sơ đồ:
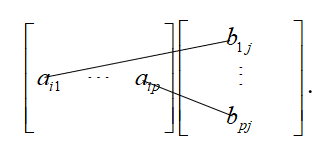
Từ đó, đưa ra câu trả lời chính xác.
