Khái niệm
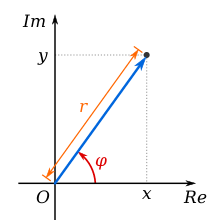
Định nghĩa: Số có dạng $x+iy$ trong đó $x,y\in\mathbb R$ được gọi là số phức. Kí hiệu $z=x+iy$.
Nếu $x=0$, tức là $z=iy$, thì $z$ được gọi là số thuần ảo.
Nếu $y=0$, tức là $z=x$, thì $z$ là một số thực.
Số phức $x-iy$, kí hiệu $\overline{z}$, được gọi là số phức liên hợp với số phức $z=x+iy$.
Quy ước: $i^2=-1$.