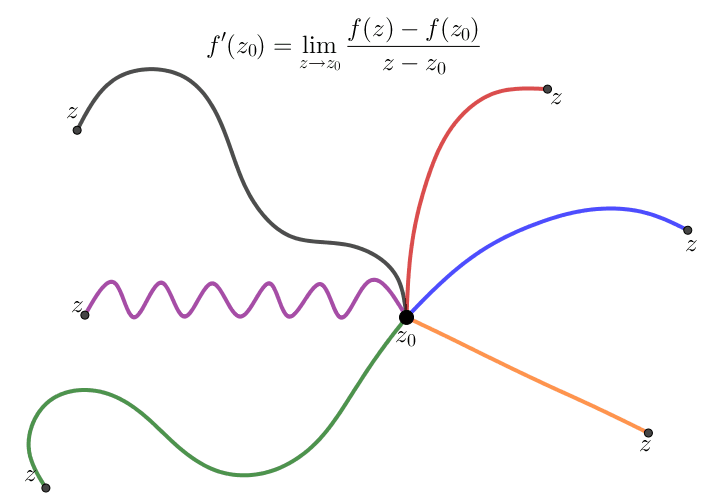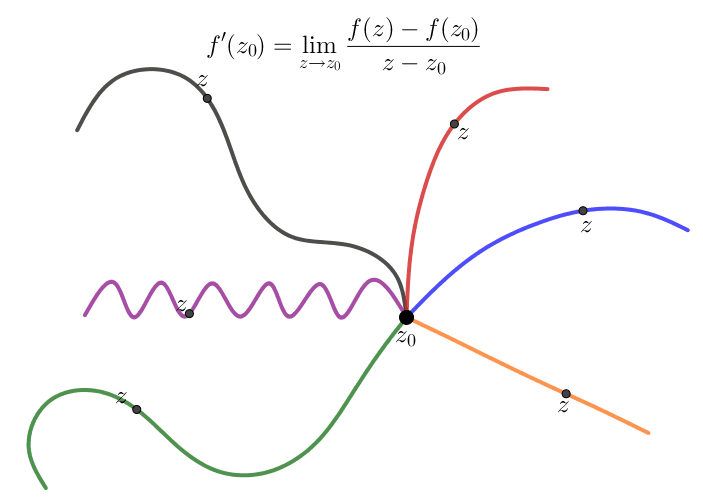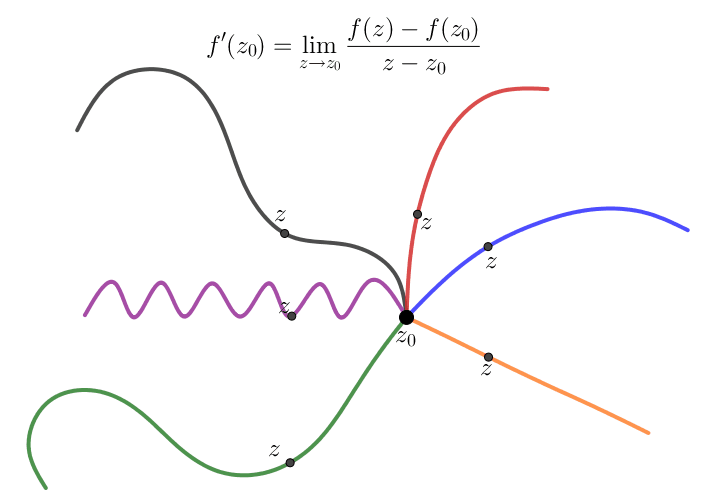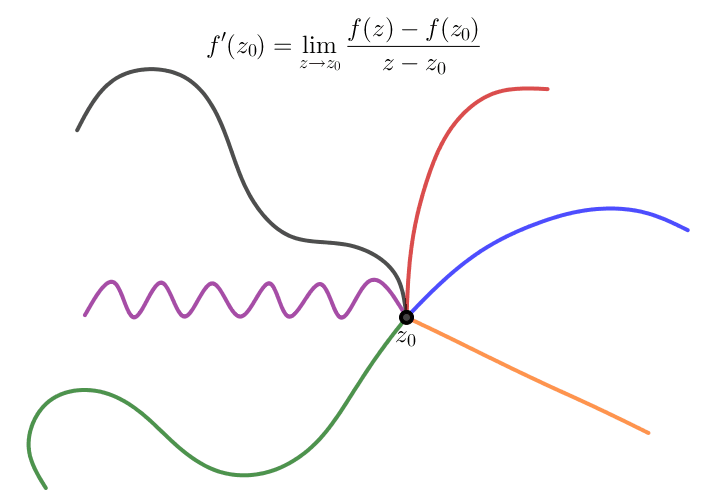
Định nghĩa
Về hình thức, ta thấy định nghĩa đạo hàm của hàm phức giống định nghĩa đạo hàm của hàm 1 biến thực, do đó với các hàm phức sơ cấp thì công thức đạo hàm tương tự hàm một biến thực. Chẳng hạn, $(z^n)'=nz^{n-1}$, $(\sin z)'=\cos z$,...
Cho $f(z)=z^2$, tính $f'(z)$.
Giải: Ta có $\Delta f=f(z+\Delta z)-f(z)=(z+\Delta z)^2-z^2=2z\Delta z+(\Delta z)^2$. Nên $\dfrac{\Delta f}{\Delta z}=2z+\Delta z$.
Do đó, $f'(z)=\lim\limits_{\Delta z\to 0}\dfrac{\Delta f}{\Delta z}=\lim\limits_{\Delta z\to 0}(2z+\Delta z)=2z$.