Tính tuyến tính
Nếu $f(t), g(t)$ có biến đổi Laplace thì với mọi hằng số $A, B$, hàm gốc $Af(t)+Bg(t)$ cũng có biến đổi Laplace và $$L\{Af(t)+Bg(t)\}=AL\{f(t)\}+BL\{g(t)\}.$$ Ví dụ: $L\{5+4\sin t\}=5L\{1\}+4L\{\sin t\}=\dfrac{5}{s}+\dfrac{4}{s^2+1}$.
Tính đồng dạng
Nếu $F(s)=L\{f(t)\}$ thì với mọi $a>0$ ta có $$L\{f(at)\}=\dfrac{1}{a}F\left(\dfrac{s}{a}\right).$$ Ví dụ: $L\{\sin at\}=\dfrac{1}{a}\dfrac{1}{(s/a)^2+1}=\dfrac{a}{s^2+a^2}$.
Tính dịch chuyển ảnh
Nếu $F(s)=L\{f(t)\}$ thì với mọi $a\in\mathbb R$ ta có $$L\{e^{at}f(t)\}=F(s-a).$$ Ví dụ: $L\{e^{at}\sin \omega t\}=\dfrac{\omega}{(s-a)^2+\omega^2}$.
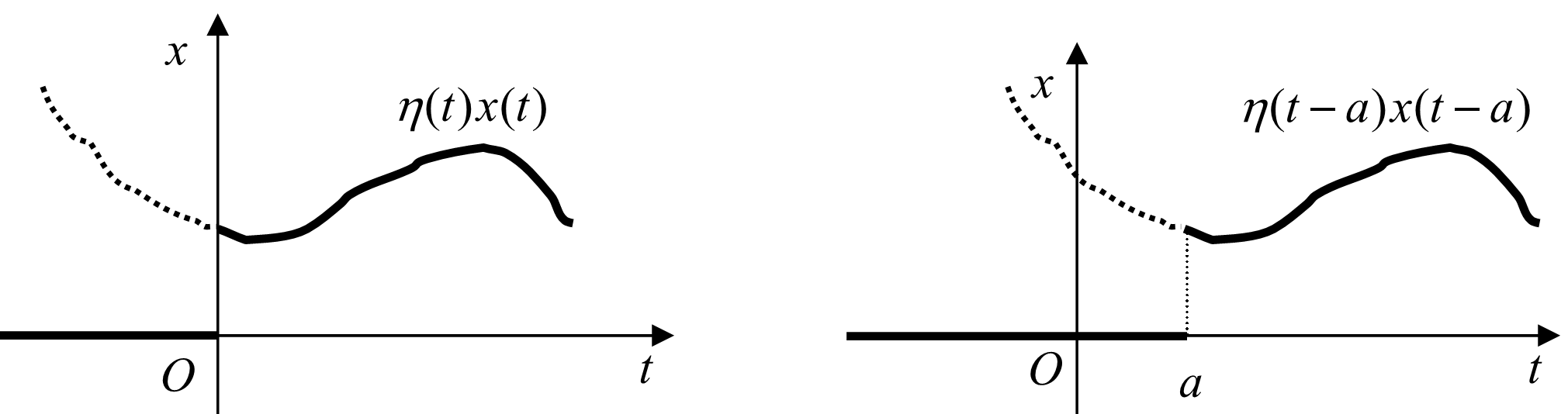
Tính trễ
Nếu $F(s)=L\{f(t)\}$ thì với mọi $a\in\mathbb R$ ta có $$L\{\eta(t-a)f(t-a)\}=e^{-sa}F(s).$$ Chú ý: Đồ thị của hàm $\eta(t-a)f(t-a)$ có được bằng cách tịnh tiến đồ thị của $\eta(t)f(t)$ dọc theo trục hoành một đoạn bằng. Nếu $f(t)$ biểu diễn tín hiệu theo thời gian $t$ thì $f(t-a)$ biểu diễn trễ $a$ đơn vị thời gian của quá trình trên.
Ví dụ: $L\{\eta(t-a)\}=L\{\eta(t-a).1\}=\dfrac{e^{-as}}{s}$.





