Khái niệm giới hạn dãy số phức

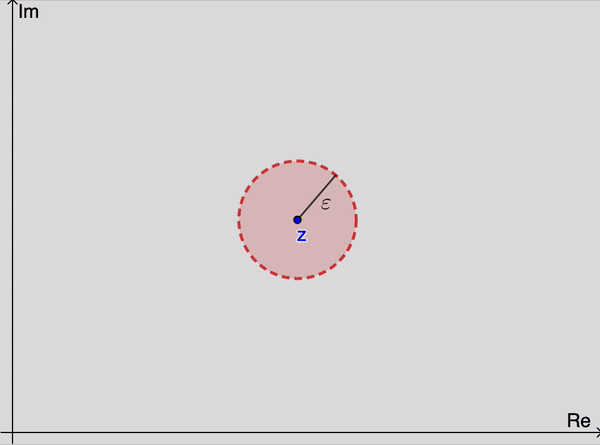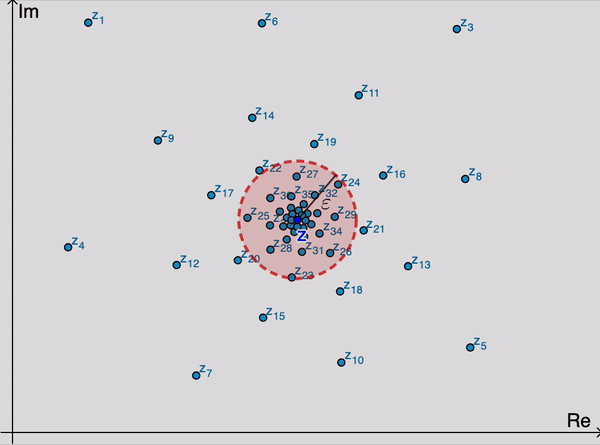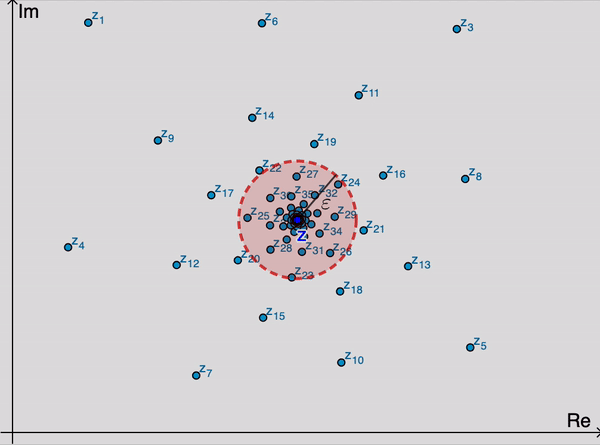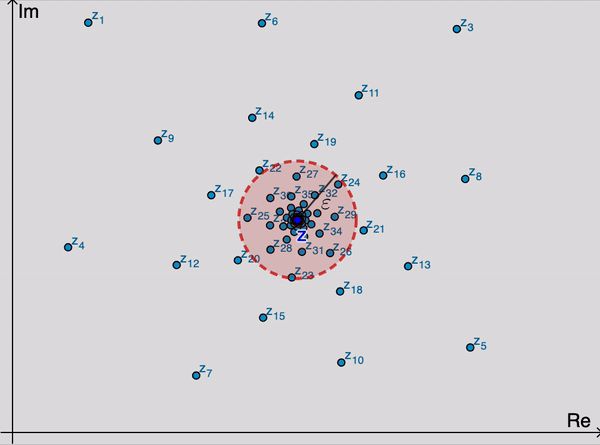
Dãy số phức $\{z_n=x_n+iy_n\}_{n=1}^\infty\to z(=a+ib), n\to \infty$ nếu $\lim\limits_{n\to\infty}|z_n-z|=0$ hoặc nếu $x_n\to a, y_n\to b, n\to\infty$. Về mặt hình học, với mọi $\varepsilon>0$, khi $n$ đủ lớn (tồn tại $n_0$ phụ thuộc vào $\varepsilon$) sao cho $z_n$ chui vào $\varepsilon$-lân cận của $z$, tức là $|z_n-z|<\varepsilon$ với mọi $n\geq n_0$. Khái niệm giới hạn của dãy số phức có thể hiểu giống khái niệm giới hạn của dãy điểm $M_n(x_n,y_n)$ hội tụ về $M_0(x_0,y_0)$ trong giải tích 2 biến.

Khái niệm giới hạn hàm phức

Hàm biến phức $f(z)$ xác định trong một lân cận của $z_0$ có giới hạn là $A$ khi $z\to z_0$, nếu: $\forall \varepsilon>0$, $\exists\delta>0$ sao cho $\forall z$ thỏa mãn $0<|z-z_0|<\delta$ thì $ |f(z)-A|<\varepsilon$.

Kí hiệu: $\lim\limits_{z\to z_0}f(z)=A$.

Tính chất

Nếu các hàm $f(z)$ và $g(z)$ có giới hạn khi $z\to z_0$ thì ta có các khẳng định sau:

1. $\lim \limits_{z \rightarrow z_0}(f(z) \pm g(z)) = \lim \limits_{z \rightarrow z_0}f(z) \pm \lim \limits_{z \rightarrow z_0}g(z)$,
2. $\lim \limits_{z \rightarrow z_0}(f(z).g(z)) = \lim \limits_{z \rightarrow z_0}f(z).\lim \limits_{z \rightarrow z_0}g(z)$,
3. $\lim \limits_{z \rightarrow z_0}\dfrac{f(z)}{g(z)} = \dfrac{\lim \limits_{z \rightarrow z_0}f(z)}{\lim \limits_{z \rightarrow z_0}g(z)},\quad (\lim \limits_{z \rightarrow z_0}g(z) \neq 0)$,
4. $\lim \limits_{z \rightarrow z_0}|f(z)| = |\lim \limits_{z \rightarrow z_0}f(z)|, \quad \text{nếu } \exists \lim \limits_{z \rightarrow z_0}|f(z)|$.