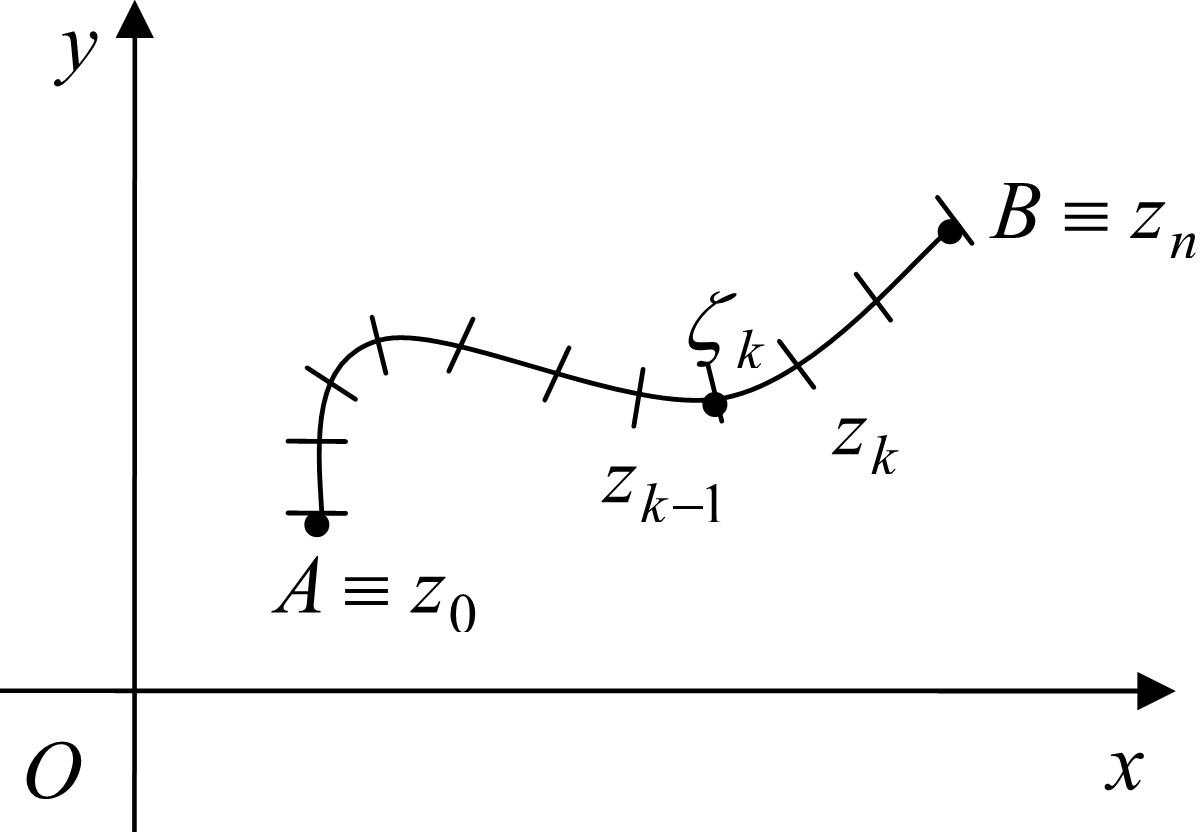
3.1. Định nghĩa
Cách tính
Cách 1:
Tổng tích phân \eqref{s1} có thể phân tích thành tổng của 2 tổng tích phân như sau:
\begin{align}\sum\limits_{k=1}^nf(\zeta_k)\Delta z_k&=\sum\limits_{k=1}^n\left[u(\xi_k,\eta_k)+iv(\xi_k,\eta_k)\right](\Delta x_k+i\Delta y_k)\\&=\sum\limits_{k=1}^n\left[u(\xi_k,\eta_k)\Delta x_k-v(\xi_k,\eta_k)\Delta y_k\right]+i\sum\limits_{k=1}^n\left[v(\xi_k,\eta_k)\Delta x_k+u(\xi_k,\eta_k)\Delta y_k\right]\tag{3.2}\label{s2}\end{align}
Hơn nữa $$\max\limits_{1\leq k\leq n}|\Delta z_k|\to 0\Leftrightarrow \begin{cases}\max\limits_{1\leq k\leq n}|\Delta x_k|\to 0\\\max\limits_{1\leq k\leq n}|\Delta y_k|\to 0\end{cases}.$$ Vì vậy, từ \eqref{s2} ta có $$\int\limits_{\overset{\huge\frown}{AB}} f(z) dz=\int\limits_{\overset{\huge\frown}{AB}}udx-vdy+i\int\limits_{\overset{\huge\frown}{AB}}vdx+udy.$$
Tính chất:
- $\int\limits_{\overset{\huge\frown}{AB}}[f(z)+g(z)]dz=\int\limits_{\overset{\huge\frown}{AB}}f(z)dz+\int\limits_{\overset{\huge\frown}{AB}}g(z)dz$,
- $\int\limits_{\overset{\huge\frown}{AB}}kf(z)dz=k\int\limits_{\overset{\huge\frown}{AB}}f(z)dz$, với $k\in\mathbb R$ là hằng số,
- $\int\limits_{\overset{\huge\frown}{AB}}f(z)dz=-\int\limits_{\overset{\huge\frown}{BA}}f(z)dz$.
Ví dụ: Tính tích phân $\int\limits_{\overset{\huge\frown}{AB}}z^2dz$ với $A=1+i$ và $B=2+4i$
a) Dọc theo parabol $y=x^2$,
b) Dọc theo đường thẳng nối $A$ và $B$.
| Ta có \begin{align}I&=\int\limits_{\overset{\huge\frown}{AB}}z^2dz=\int\limits_{\overset{\huge\frown}{AB}}(x+iy)^2(dx+idy)\\&=\int\limits_{\overset{\huge\frown}{AB}}(x^2-y^2)dx-2xydy+i\int\limits_{\overset{\huge\frown}{AB}}2xydy+(x^2-y^2)dx.\end{align}a) Nếu lấy dọc theo $y=x^2$ thì $dy=2xdx$, khi đó $$I=\int_1^2 (x^2-5x^4)dx+i\int_1^2(4x^3-2x^5)dx=-\dfrac{86}{3}-6i.$$b) Nếu lấy tích phân dọc theo đường thẳng nối từ A đến B thì $y=3x-2$ và $dy=3dx$, khi đó $$I=\int_1^2(24x-26x^2-4)dx+i\int_1^2(32x-18x^2-12)dx=-\dfrac{86}{3}-6i$$ | 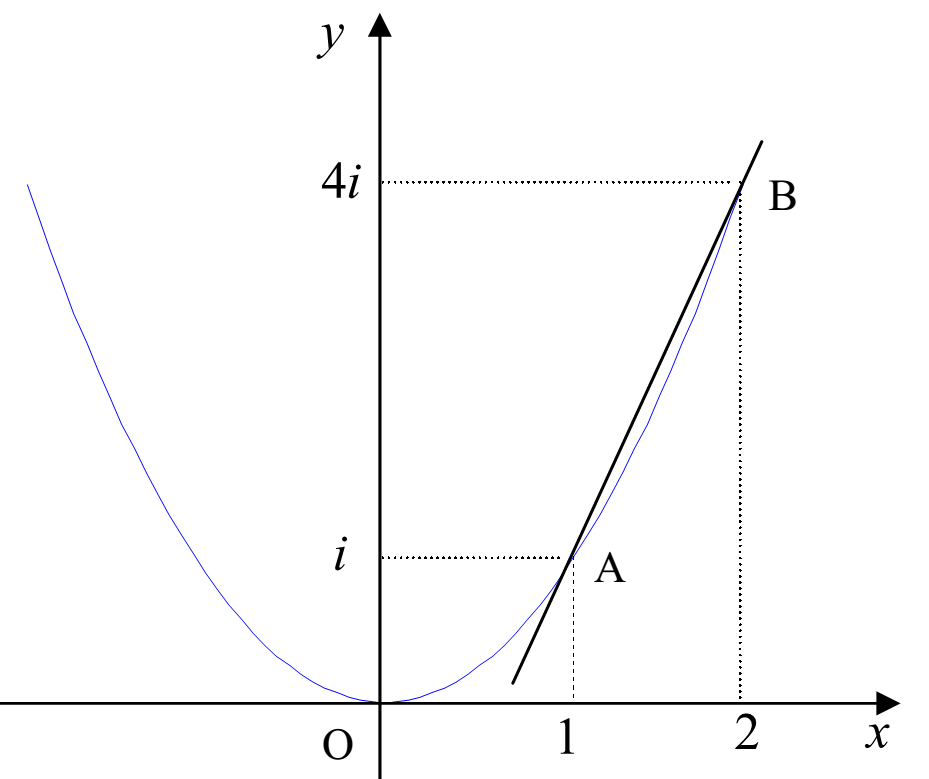 |
Cách 2:
Xét hàm phức $f(z)$ xác định và liên tục trên cung $\gamma$ bất kì trơn từng khúc và có phương trình tham số $z=\gamma(t)$ với $a\leq t\leq b$. Tức là $\gamma: [a,b]\to\mathbb C$ là hàm liên tục. Ở đây $\gamma(t)=x(t)+iy(t)$ với $x, y$ là các hàm 1 biến thực, hơn nữa $\gamma'(t)=x'(t)+iy'(t)$ tồn tại tại các điểm trong $[a,b]$ ngoại trừ tại hữu hạn điểm $t_1,t_2,\cdots,t_n$ và nếu tại các điểm tồn tại đạo hàm thì các đạo hàm đó cũng liên tục.
|
|
|
|
|
Khi đó ta có $$\int_\gamma f(z)dz=\int_a^bf(z(t))z'(t)dt.$$
Ví dụ: Tính $\int_C\overline{z}dz$ với $C$ là đường cong cho bởi phương trình tham số $x(t)=3t, y(t)=t^2$, trong đó $t\in[-1,4]$.
| Ta có $C$ là đường cong $\gamma(t)=x(t)+iy(t)=3t+it^2$. Như vậy $f(z)=f(\gamma(t))=\overline{3t+it^2}=3t-it^2$. Suy ra $dz=(3-i2t)dt$. Vậy \begin{align}\int_C\overline{z}dz&=\int_{-1}^4(3t-it^2)(3-i2t)dt\\&=\int_{-1}^4 \left(2t^3+9t + 3t^2i\right)dt=195+ 65 i\end{align} | 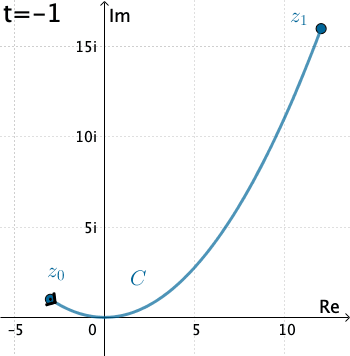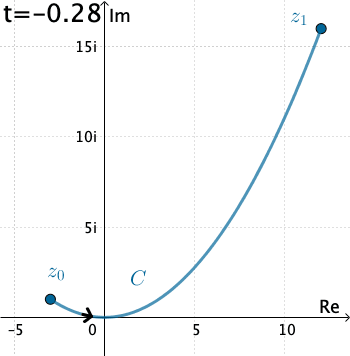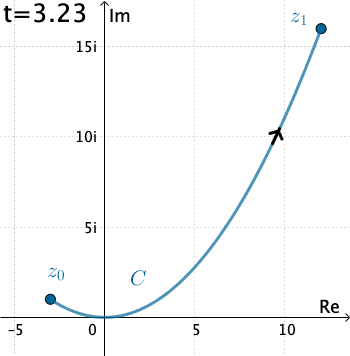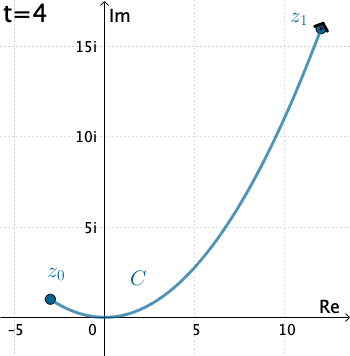 |
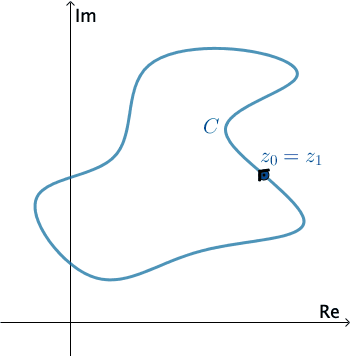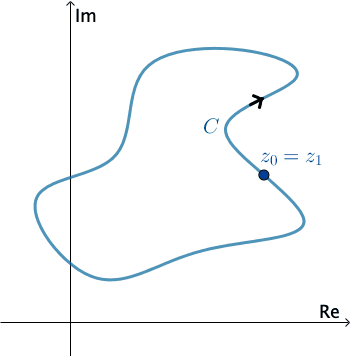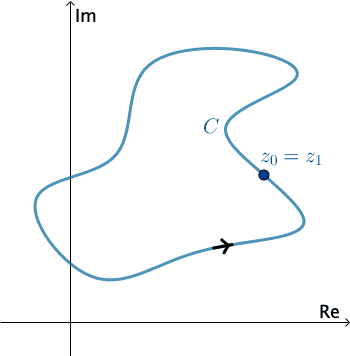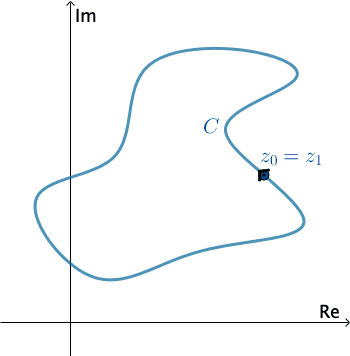
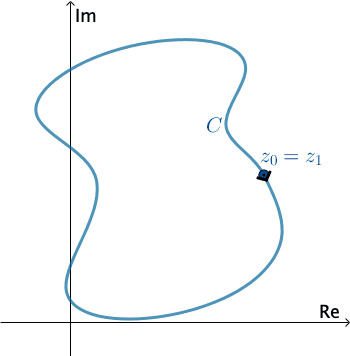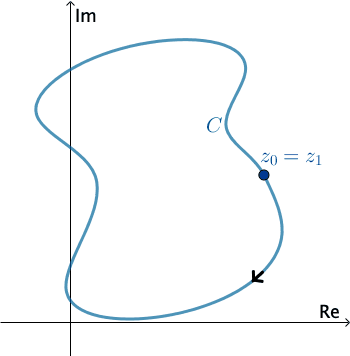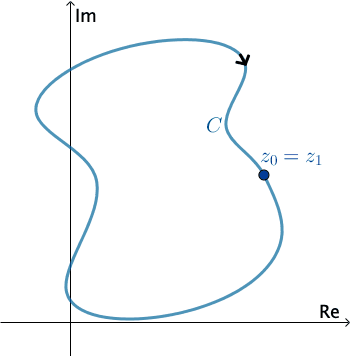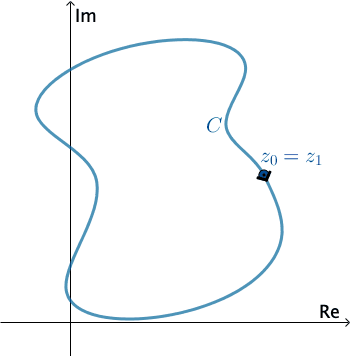
Tích phân trên đường cong kín
Nếu $\gamma$ là 1 cung kín, ta kí hiệu $\oint\limits_\gamma f(z)dz$ và chiều lấy tích phân trên $\gamma$ là chiều dương.
|
|
Ví dụ: Tính $\int\limits_C\dfrac{1}{z}dz$ với $C(O;1)$ (đường tròn tâm $O$, bán kính 1).
Bước 1Tham số hóa đường cong: $x(t)=\cos t$, $y(t)=\sin t$ với $t\in[0,2\pi]$, khi đó $z(t)=ie^{it}dt$ Bước 2Tính $dz=ie^{it}dt$. Bước 3Viết lại công thức tích phân: $$I=\int_C\dfrac{1}{z}dz=i\int_0^{2\pi}\dfrac{1}{e^{it}}e^{it}dt=2\pi i.$$ |
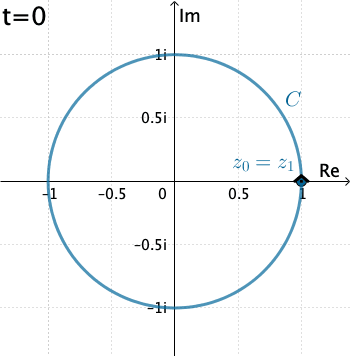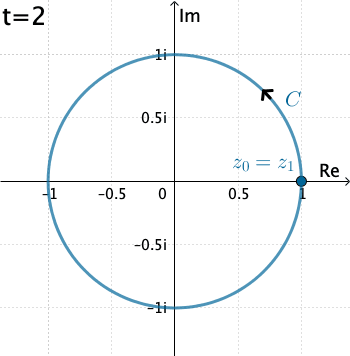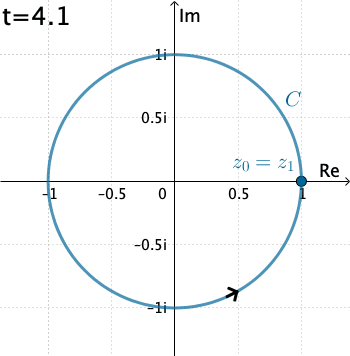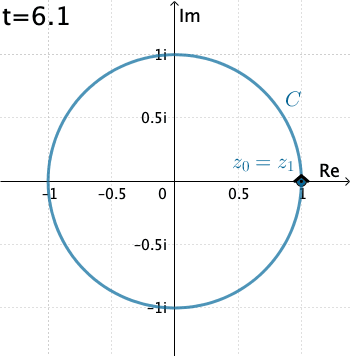 |