Định lí: Điều kiện cần và đủ để tích phân của hàm $f(z)$ trong miền $D$ không phụ thuộc vào đường lấy tích phân là tích phân của $f(z)$ dọc theo mọi đường cong kín bất kỳ (không tự cắt nhau) trong $D$ phải bằng 0, tức là $$\oint_\gamma f(z)dz=0,\text{ với mọi }\gamma\subset D.$$
|
|
|
|
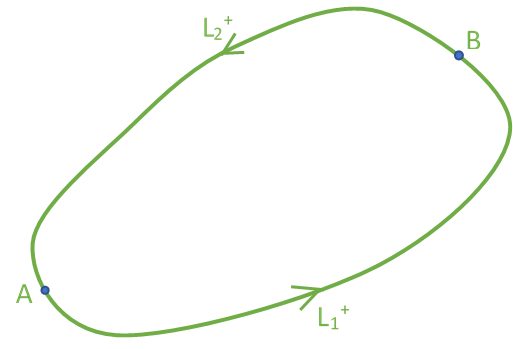
Ta có $$0=\int\limits_L f(z)dz=\int\limits_{L_1^+}f(z)dz+\int\limits_{L_2^+}f(z)dz=\int\limits_{L_1^+}f(z)dz-\int\limits_{L_2^-}f(z)dz.$$ Nên $\int\limits_{L_1^+}f(z)dz=\int\limits_{L_2^-}f(z)dz$, hay tích phân không phụ thuộc vào đường đi, chỉ phụ thuộc vào điểm đầu $A$ và điểm cuối $B$. |
|
Định lí: Nếu hàm phức $f(z)$ giải tích trong miền đơn liên $D$ thì tích phân của $f(z)$ dọc theo mọi đường cong kín $\gamma$ bất kỳ trong $D$ đều bằng 0.
Hệ quả:
1. Nếu $f(z)$ giải tích trong miền kín, đơn liên $\overline{D}=D\cup \partial D$ (gồm miền trong $D$ và biên $\partial D$) thì $\int\limits_{\partial D}f(z)dz=0$.
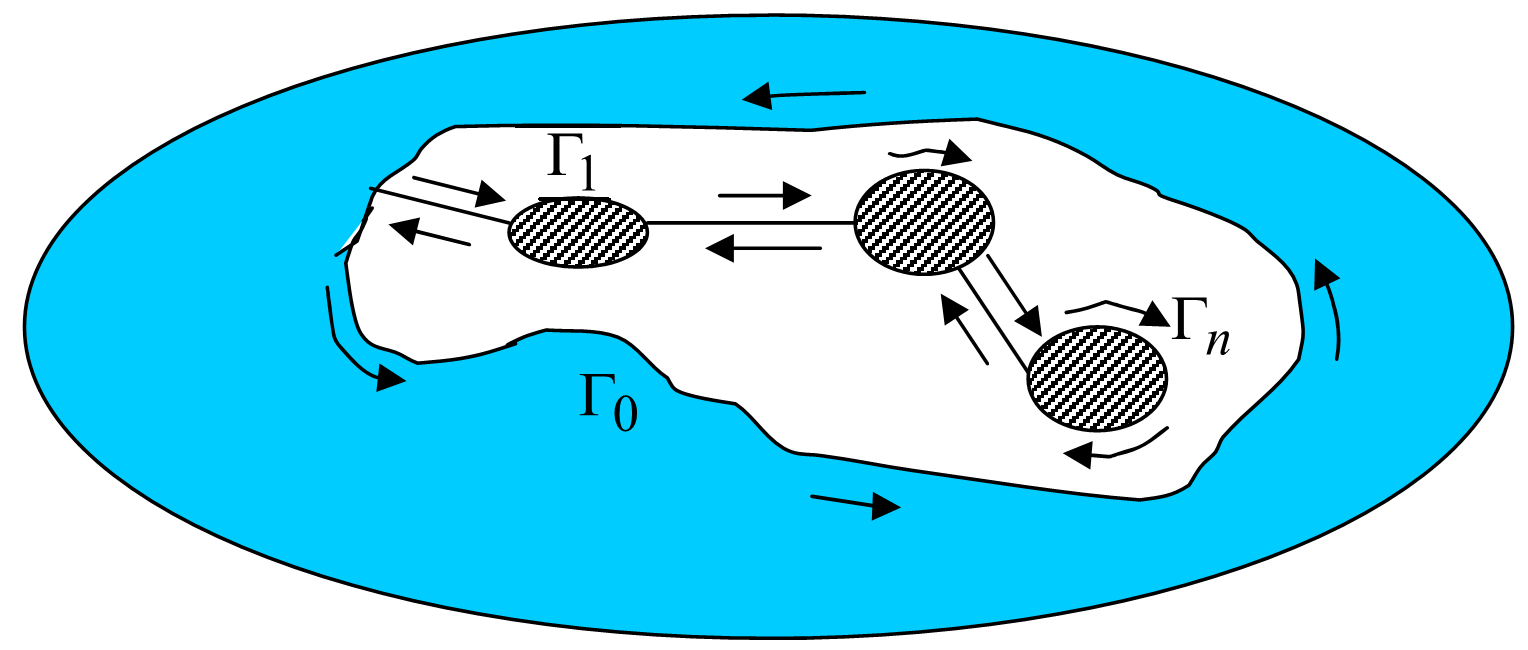
| 2. Giả sử hàm $f(z)$ giải tích trong miền kín đa liên $\overline{D}$ có biên ngoài là $\Gamma_0$ và biên trong là $\Gamma_1,\cdots,\Gamma_n$ thì $$\oint\limits_{\Gamma_0}f(z)dz=\sum\limits_{k=1}^n\oint\limits_{\Gamma_k}f(z)dz.$$ |
|
Ví dụ: Tính tích phân $I_n=\oint\limits_L\dfrac{dz}{(z-a)^n},n\in\mathbb Z$ trong đó $L$ là đường cong kín bất kỳ không đi qua $a$.
Gọi $D$ là miền được giới hạn bởi $L$. Ta có 2 trường hợp:
- $a\notin D$ thì $f(z)=\dfrac{1}{(z-a)^n}$ giải tích trong $D$ nên $I_n=0$.
- $a\in D$. Gọi $C_r=\{z\in\mathbb C: |z-a|=r\}$ là đường tròn tâm $a$, bán kính $r$. Chọn $r$ đủ bé để $C_r\subset D$. Xét $D'$ là miền nhị liên có được bằng cách lấy miền $D$ bỏ đi hình tròn tâm $a$ bán kính $r$. $D'$ có biên ngoài là $L$, biên trong là $C_r$. Hàm $f(z)=\dfrac{1}{(z-a)^n}$ giải tích trong $D'$. Theo hệ quả 2 ta có: $$I_n=\oint\limits_L\dfrac{dz}{(z-a)^n}=\oint\limits_{C_r}\dfrac{dz}{(z-a)^n}.$$ Phương trình tham số của $C_r$ là: $z=a+re^{it}$ với $t\in[0,2\pi]$. Khi đó $$I_n=\int\limits_0^{2\pi}\dfrac{rie^{it}}{r^ne^{int}}dt=\begin{cases}i\int\limits_0^{2\pi}dt&\text{khi }n=1\\\text{}\\\dfrac{1}{r^{n+1}}\int\limits_0^{2\pi}e^{i(1-n)t}dt&\text{khi }n\neq 1\end{cases}=\begin{cases}2\pi i&\text{khi }n=1\\0&\text{khi }n\neq 1\end{cases}.$$