7.4. Một số phân phối thông dụng

Quy luật phân phối nhị thức

Giả sử ta tiến hành $n$ phép thử lặp, độc lập, một biến cố $A$ nào đó mà ta cần quan tâm. Trong mỗi phép thử chỉ có thể xảy ra 1 trong 2 trường hợp là hoặc $A$ xảy ra hoặc $A$ không xảy ra, $A$ xảy ra với $P(A) = p$. Gọi $X=$ “số lần xảy ra của biến cố $A$ trong $n$ phép thử” thì BNN $X$ là rời rạc và nó có thể nhận 1 trong các giá trị: $0, 1, 2, \cdots, n$ với các xác suất tương ứng được tính theo công thức Bernoully: $$p_k=p(X=k)=C_{n}^{k}p^k(1-p)^{n-k}\tag{*}\label{7.4},\quad \text{với }k=0,1,2,\cdots,n.$$

Định nghĩa: Biến ngẫu nhiên rời rạc $X$ nhận 1 trong các giá trị $0, 1, \cdots, n$ với các xác suất tương ứng được tính theo công thức \eqref{7.4} gọi là tuân theo quy luật phân phối nhị thức với các tham số $n$ và $p$, ký hiệu là $B(n,p)$.

Bảng phân phối xác suất của ĐLNN $X$ có phân phối nhị thức $B(n,p)$

$X$	0	1	$\cdots$	$k$	$\cdots$	$n$
$p(x)$	$(1-p)^n$	$C^1_np(1-p)^{n-1}$	$\cdots$	$C^k_np^k(1-p)^{n-k}$	$\cdots$	$p^n$

Các tham số đặc trưng: $E(X)=np$, $D(X)= np(1-p)$, $\sigma(X)=\sqrt{np(1-p)}$.

Quy luật phân phối chuẩn (phân phối Gauss)

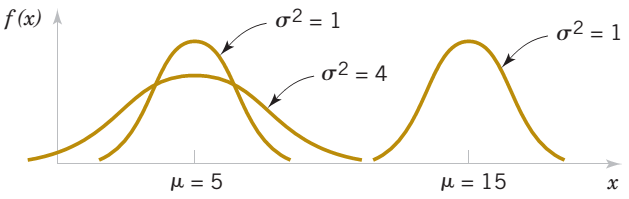
Định nghĩa: Biến ngẫu nhiên $X$ nhận giá trị trong $(-\infty , +\infty)$ được gọi là tuân theo quy luật phân phối chuẩn hay quy luật phân phối Gauss, ký hiệu là $N(\mu,\sigma^2)$ nếu hàm mật độ xác suất của $X$ có dạng sau: $f(x)= \dfrac{1}{\sqrt{2\pi}\sigma}\exp\left(-\dfrac{(x-\mu)^2}{\sigma^2}\right)$.

Chú ý: Đồ thị của hàm mật độ của phân phối chuẩn có hình cái chuông, và bởi vậy phân phối này còn được gọi là phân phối hình chuông. Trung điểm của cái chuông này chính là điểm $x = \mu$, và độ cao của chuông chính bằng $\dfrac{1}{\sigma\sqrt{2\pi}}$. Nếu $\sigma$ càng nhỏ thì chuông càng cao và càng "hẹp", ngược lại $\sigma$ càng lớn thì chuông càng thấp và càng rộng ra.

Các tham số đặc trưng: $E(X) = \mu$, $D(X) = \sigma^2$, $\sigma(X)=\sigma$.

Xem đồ thị và tra bảng các giá trị tới hạn của phân phối chuẩn.

Quy luật phân phối chuẩn tắc

Định nghĩa: Biến ngẫu nhiên $X$ tuân theo quy luật phân phối chuẩn với $E(X)=0, D(X) = 1$ thì BNN $X$ được gọi là tuân theo quy luật phân phối chuẩn tắc, ký hiệu là $N(0, 1)$.

 Hàm mật độ của phân phối chuẩn tắc kí hiệu là $\varphi(x)$ cho bởi: $$\varphi(x)=\dfrac{1}{\sqrt{2\pi}}\exp\left(-\dfrac{x^2}{2}\right).$$

Hàm phân phối của phân phối chuẩn tắc kí hiệu là $\Phi(x)$ có biểu thức $$\Phi(x)=\dfrac{1}{\sqrt{2\pi}}\int_{-\infty}^x\exp\left(-\dfrac{t^2}{2}\right)dt,\quad \forall x\in\mathbb R.$$

Hàm phân phối $\Phi(x)$ có tính chất sau: $\Phi(-x)=1-\Phi(x)$, Nếu $X$ có phân phối $N(0,1)$ thì với mọi $a>0$, ta có $$P(|X|>a)=2(1-\Phi(a))\quad \text{và}\quad P(|X|<a)=2\Phi(a)-1.$$

Định nghĩa: Giá trị $U_\alpha$ được gọi là giá trị tới hạn mức $\alpha$ của phân phối chuẩn tắc nếu $\Phi(U_\alpha)=1-\alpha$.

Chú ý:

1. Nếu $X$ có phân phối $N(0,1)$ thì với mọi $\alpha\in (0,1)$, ta có: $$P(X>U_\alpha)=P(|X|>U_{\alpha/2})=\alpha\quad\text{và}\quad P(|X|<U_{\alpha/2})=1-\alpha.$$
2. Nếu $X\sim N(\mu;\sigma^2)$ thì $\dfrac{X-\mu}{\sigma}\sim N(0,1)$, khi đó
   • $P(X\leq a)=P\left(\dfrac{X-\mu}{\sigma}\leq \dfrac{a-\mu}{\sigma}\right)=\Phi\left(\dfrac{a-\mu}{\sigma}\right)$,
   • $P(\alpha\leq X\leq \beta)=P\left(\dfrac{\alpha-\mu}{\sigma}\leq \dfrac{X-\mu}{\sigma}\leq \dfrac{\beta-\mu}{\sigma}\right)=\Phi\left(\dfrac{\beta-\mu}{\sigma}\right)-\Phi\left(\dfrac{\alpha-\mu}{\sigma}\right)$,
   • $P(|X-\mu|<\varepsilon)=P\left(\left|\dfrac{X-\mu}{\sigma}\right|<\dfrac{\varepsilon}{\sigma}\right)=2\Phi\left(\dfrac{\varepsilon}{\sigma}\right)-1$.

Ví dụ:  Gọi $X$ là chỉ số thông minh (IQ) của học sinh trung học cơ sở. Giả sử $X\sim N(85;25)$.

1. Tính xác suất chọn được học sinh rất thông minh, hiểu là $X\geq 90$.
2. Tính tỉ lệ học sinh trong lứa tuổi này có chỉ số IQ thuộc $(80;95)$.
3. Gọi $Y$ là số học sinh có IQ thuộc $(80; 95)$ trong lớp 50 học sinh. Hãy chỉ rõ luật phân phối xác suất của $Y$.
4. Trong một lớp gồm 50 học sinh thì trung bình có bao nhiêu em rất thông minh $(X\geq 90)$? Con số trung bình tìm được có phải là số có khả năng xảy ra cao nhất hay không? Vì sao?