|
Tọa độ trụ của một điểm $M(x,y,z)$ trong không gian $Oxyz$ là 1 bộ có thứ tự gồm 3 số $(r,\varphi ,z)$ trong đó $(r,\varphi )$ là các tọa độ cực của điểm $M'(x,y)$ (là hình chiếu vuông góc của $M(x,y,z)$ lên mặt phẳng tọa độ $Oxy$. Với mọi điểm của không gian ta có $r\ge 0;{\rm \; }\varphi \in {\rm [}0,2\pi );{\rm \; }z\in (-\infty ,+\infty )$. |
|
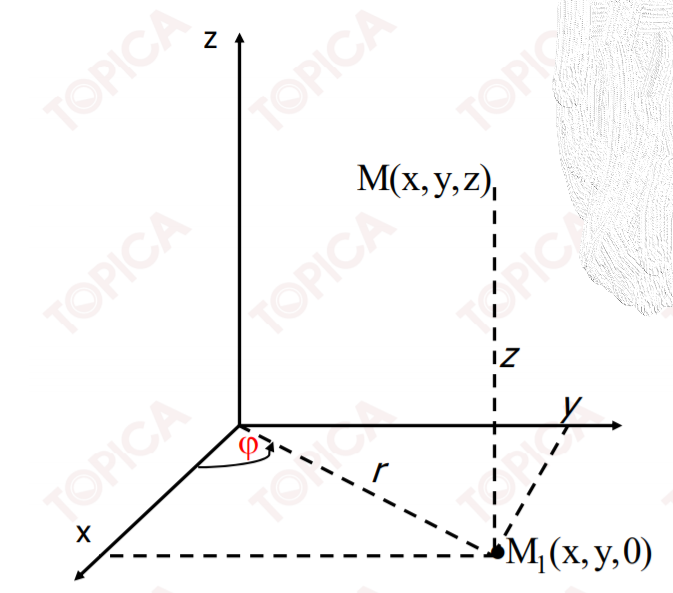
Quan hệ giữa các tọa độ đề các $x,y,z$ và các tọa độ trụ $r,\varphi ,z$ của cùng một điểm $M$: $\left\{\begin{array}{l} {x=r\cos \varphi } \\ {y=r\sin \varphi } \\ {z=z} \end{array}\right. $ (**)
Nếu $r>0;{\rm \; }\varphi \in {\rm [}0,2\pi );{\rm \; }z\in (-\infty ,+\infty )$ thì các công thức (**) xác định 1 song ánh giữa các tọa độ Đề Các và tọa độ trụ (riêng các điểm trên trục $Oz$ có $z$ xác định, $r=0$, $\varphi $ tùy ý).
Xem các công thức $\left\{\begin{array}{l} {x=r\cos \varphi } \\ {y=r\sin \varphi } \\ {z=z} \end{array}\right. $ như một phép đổi biến, ta có:
$J=\dfrac{D(x,y,z)}{D(r,\varphi ,z)} =\left|\begin{array}{ccc} {\cos \varphi } & {-r\sin \varphi } & {0} \\ {\sin \varphi } & {r\cos \varphi } & {0} \\ {0} & {0} & {1} \end{array}\right|=r\ne 0$ (trừ những điểm trên trục $Oz$). Ta có công thức $$\iiint\limits _{Q}f(x,y,z)dxdydz =\iiint\limits _{Q'}f(r\cos \varphi ,r\sin \varphi ,z)rdrd\varphi dz. \label{9.3.6}\tag{6}$$
Tính tích phân $\iiint\limits _{Q}z(x^{2} +y^{2} )dxdydz $ với $Q$ được giới hạn bởi các mặt $x^{2} +y^{2} =1;{\rm \; }z=0;{\rm \; }z=2$.
$Q$ là hình trụ tròn xoay $0\le r\le 1;{\rm \; }0\le z\le 2$, nên việc tính toán sẽ đơn giản nếu chuyển sang tọa độ trụ và áp dụng công thức \eqref{9.3.7}. Ta có: $$\iiint\limits _{V}z(x^{2} +y^{2} )dxdydz =\int _{0}^{2\pi }d\varphi \int _{0}^{2}zdz \int _{0}^{1}r^{3} dr =\pi. $$
Tính tích phân $\iiint\limits _{Q}\sqrt{x^{2} +y^{2}}dxdydz$ với $Q$ được giới hạn bởi các mặt $x^{2} +y^{2} =2y; z=0; z=2$.
Ta có, miền $Q$: $x^{2}+(y-1)^{2}=1; z=0; z=2$ là hình trụ tròn xoay, có hình chiếu vuông góc lên mặt phẳng $Oxy$ là miền $D$-hình tròn tâm $I(0,1)$ bán kính $R=1$, nên việc tính toán sẽ đơn giản nếu chuyển sang tọa độ trụ và áp dụng công thức \eqref{9.3.6} với $Q'=\left\{(r,\varphi,z)|0\le r\le 2\sin \varphi ;{\rm \; }0\le \varphi \le \pi ;{\rm \; }0\le z\le 2\right\}.$ Ta có: $$\iiint\limits _{Q}\sqrt{x^{2} +y^{2} } dxdydz =\iiint\limits _{Q'}r^{2} drd\varphi dz =\int _{0}^{\pi }d\varphi \int _{0}^{2}dz \int _{0}^{2\sin \varphi }r^{2} dr =\dfrac{64}{9}.$$
